Now that you’ve gotten your pond built, it might be a wise idea to know how to calculate pond volume both based on total pond square footage and pond volume. Sure you can find an automatic pond volume calculator online somewhere, but it pays to have the calculations referenced and at least understand how they work.
How To Calculate Pond Square Footage
Let’s talk about the square footage of your pond first, since that’s going to be the first piece of information you might need to know. It does not matter whether you are lining your pond with a rubber liner, Polyurea, or you plan a structured pond that can be waterproofed with Pond Shield Epoxy. In all of these scenarios, you will still need to calculate the total square feet of the pond.
There are some very basic shape categories that almost any pond shape will fall into. Circles, ellipses, rectangles, polygons, general triangles and right triangles. If you have trouble deciding, picture your pond as though you were floating above and looking down at it.
One point I would like to bring up before we move forward is the actual volume of a single cubic foot. One single cubic foot will hold 7.48 gallons of water. As a side note, one gallon of water weighs 8.4 pounds. One cubic foot of water volume would weigh almost 63 pounds. That does not sound like much now, but just wait until you see how many cubic feet of volume your pond ends up being!
Today, I would like to talk about calculating square footage and then we’ll move onto calculating volume for circular ponds. These are pretty basic shapes and the formulas are pretty simple. Typical terminology for circles would be radius, diameter and circumference and for volume you’ll use height. Of course then there is also Pi.
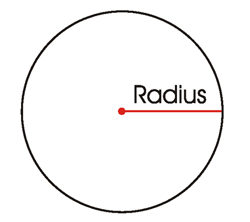
- Radius – The radius of a circle is measured as exactly one half of the diameter.
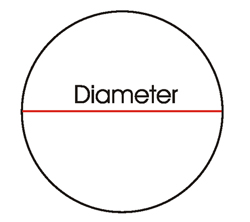
- Diameter – The diameter of a circle is measured as the length from one side of a circle to the other side, using the center as an intersection point.
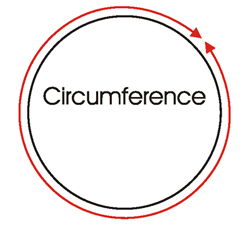
- Circumference – The circumference of a pond is the measurement of the outside shape or outline of the circle.
- Height – This is simple, it is the measurement of how high the walls of the circle are.
- Pi – This is my favorite. It even has a symbol
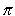It represents the ratio of any circle’s circumference in relation to its diameter. Confused yet? Not to worry. For the most part, it will be represented as a number in our calculations with and that number is 3.14.
With that being said, let’s see what we can do with that information. If you plan to calculate the total square footage of your circular pond, you have to know the radius, the circumference and the height. So let’s say that your pond has a height of 3 feet, a radius of 10 feet, meaning that from side to side it is 20 feet (diameter). Knowing this will enable you to figure out the circumference. Let’s say that:
Height = 3 feet
Radius = 10 feet
Radius x 2 = Diameter (20 feet) Just showing you this so that you see how radius and diameter relate to one another
10 x 2 = 20
Circumference (62.8) = Pi (= 3.14) x Diameter (20) Multiply the radius times two in order to find the diameter and then multiply the diameter times Pi and you will have the circumference.
62.8 = 3.14 x 20
To calculate the square footage of the walls of the circle, you multiple the circumference by the height.
62.8 x 3 = 188.4
The floor of the pond would be calculated by multiplying the radius by the radius and then multiplying that total by Pi.
10 x 10 x 3.14 = 314
Finally the total square footage of the circular pond would be the total area of the floor added to the total square footage of the walls.
188.4 + 314 = 502.4 square feet
Now to figure out how many kits of Pond Shield Epoxy you are going to need to coat the project, divide the total number of square feet a kit will yield by the total square feet of the pond.
A quart and a half kit yields 60 square feet of material at a thickness of 10 mils. 10 mils is the recommended minimum thickness that the epoxy should be applied. So,
502.4 / 60 = 8.37 kits (round that up to 9 total quart and a half kits)
Fortunately, the volume of this type of shape is simple. You already have all of the components to calculate square footage and some of those will allow us to calculate volume. In doing so, we’ll multiply the radius by the radius, and then multiply that by Pi, and finally multiply that by the height. So,
10 x10x 3.14 x 3 = 942 cubic feet
The overall weight of the water is simple too,
942 cubic feet x 8.4 pound per gallon = 7,912.80 pounds. I told you it would be a lot!
Are you ready to use our calculator to calculate your pond project now? Check out our pond volume calculator.
Check out our article on how to calculate pond volume and square footage for rectangles and our article for pond volume and square footage for ellipses.
